Dimensional Analysis
Introduction
Conversion Factors and Their
Reciprocals
Use of Conversion Factors: Some
Examples
Developing the Units Path
Summary and Helpful Hints
Introduction
Example 1: Suppose you want to convert $100 in U.S. dollars
to Canadian dollars. You know that the exchange rate is currently
$1.50 Cdn. for every $1.00 U.S. How much Canadian cash will you get?
Solution. You probably solved this in your head: you'll
expect to receive $150 Canadian for your $100 U.S. But think
carefully! This isn't intuitively obvious, you had to learn how to do
it. The steps you probably followed, so fast you didn't realize, were
these:
1. You recognized that you were starting with $100
U.S. (the starting quantity)
2. You got a conversion factor from the English sentence that
tells you the exchange rate: the conversion factor is
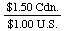
3. You then multiplied the starting quantity by the conversion
factor to get your answer (the desired quantity):
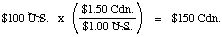
This gives us a method for solving many problems that aren't so
obvious as converting U.S. to Canadian dollars.
|
The Dimensional Analysis Method
- Identify the starting quantity. Write it down. (In
the above example, it was $100 U.S.)
- Decide what units (dimensions) you need for your
answer. Develop a path that gets you from your starting
units to the units you need. Write down the conversion
factor between the units.
- Following the "units path," multiply your starting
quantity by one or more conversion factors so that you
finally obtain the units you need. All the unwanted units
will cancel each other when you multiply.

To put it in simpler terms, we
want to know how to get from what we are GIVEN (the starting
quantity) to what we WANT TO KNOW (the desired quantity)
|
Dimensional analysis is sometimes called the factor-label
method or the factor-unit method. That is because it
involves two quantities: a mathematical proportionality that is
thefactor and an expression of the units, or label.
Conversion Factors and Their
Reciprocals
Every conversion factor has a reciprocal that can be used for the
opposite conversion. To convert $U.S. to Canadian dollars, we used
the factor
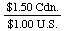
However, if we wanted to convert Canadian dollars to U.S. dollars,
we would use the reciprocal of the above factor, or
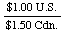
So, if we had $500 Cdn., we could determine how much U.S. money we
could get in exchange:
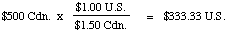
Below are some other conversion factors you will have seen in your
studies of chemistry.
|
Conversion Factor
|
Reciprocal of Conversion Factor
|
|
10 mm / cm
|
1 cm / 10 mm
|
|
453.6 g / lb
|
161 lb / 453.6 g
|
|
6.022 x 1023 atoms Cu / mol Cu
|
1 mol Cu / 6.022 x 1023 atoms Cu
|
|
63.546 g Cu / mol Cu
|
1 mol Cu / 63.546 g Cu
|
|
2 mol NaOH / mol H2SO4
|
1 mol H2SO4 / 2 mol NaOH
|
|
36.9 g Fe2O3 / 100 g ore
|
100 g ore / 36.9 g Fe2O3
|
Use of Conversion Factors: Some Examples
Example 1. (a) Write the reciprocal for the following
conversion factor: 1 mol NaOH / 40.0 g NaOH. (b) Which of these (the
original factor or its reciprocal) do we use if we want to change the
mass of NaOH (49.7 g) to moles?
Answer: (a) 40.0 g NaOH / mol NaOH
(b) the original factor: (49.7 g NaOH) x (1 mol NaOH / 40.0 g NaOH)
gives units of moles NaOH
Example 2. (a) Write the reciprocal for the following
conversion factor: 3 atoms S / molecule P4S3.
(b) Which of these (the original factor or its reciprocal) do we use
if we want to calculate how many molecules of
P4S3 can be made from a 1200 S atoms?
Answer: (a) 1 molecule
P4S3 / 3 atoms S
(b) the reciprocal factor: (1200 S atoms) x (1 molecule
P4S3 / 3 atoms S) gives units of molecules of
P4S3
Example 3. (a) Write the reciprocal of the following
conversion factor: 3 mol AgCl / mol CrCl3. (b) Which of
these (the original factor or its reciprocal) do we use if we want to
calculate how many moles of AgCl can be prepared from 0.1250 moles of
CrCl3?
Answer: (a) 1 mol CrCl3 / 3 mol
AgCl
(b) the original factor: (0.1250 mol CrCl3) x ( 3 mol AgCl
/ mol CrCl3) has units of moles AgCl
Example 4. (a) Write the conversion factor for "36.3%
chocolate chips in Chips Ahoy cookies," then write its reciprocal.
Which of these (the original or its reciprocal) do we use to
calculate how many cookies have to be processed to yield a 500. g of
chocolate chips?
Answer: (a) conversion factor is 36.3 g
chocolate chips / 100 g cookies; reciprocal is 100 g cookies / 36.3 g
chocolate chips
(b) the reciprocal factor: (500. g chocolate chips) x (100 g
cookies / 36.3 g chocolate chips) has units of mass of cookies.
Developing the Units Path: Extended
Examples
Example 1. You have 45.5 grams of iron, Fe. What mass (in
g) of Fe2O3 can you make if you react the iron
with oxygen? The balanced equation is
4 Fe + 3 O2 ---> 2
Fe2O3
Molar masses: Fe 55.85 g / mol;
Fe2O3 159.7 g / mol
Analysis: We want to know how we can get from
what we are given (45.5 g Fe) to what we WANT (mass of
Fe2O3). Now you know about chemistry and
balanced equations, so you know that the MOLE is the important unit
here, and we'll have to work through moles. If we want to get from
mass of Fe to mass of Fe2O3, we'll have to have
a bunch of conversion factors since no single factor that we've been
given can get us there.
The balanced equation gives us this conversion factor that relates
the product to the reactant: 4 mol Fe / 2 mol
Fe2O3. We have two other conversion factors,
the molar masses, that allow us to go from masses to moles and vice
versa. We also have the reciprocals of these factors.
The sequence of operations is this:
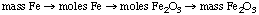
THIS SEQUENCE IS IMPORTANT! It may take a while to figure
out, and you may have to play with conversion factors to realize just
how you'll get from one step to another. But by now you'll know that
mass/mole conversions are made through the conversion factor molar
mass or its reciprocal. And the balanced equation gives you the
connection between the moles of reactants and products.
So: we begin with 45.5 g Fe, and use the above sequence with its
conversion factors chosen so that all the units cancel except "g
Fe2O3" which is what we wanted to find:
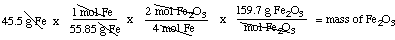
Example 2. You are a chemist in an ore-processing plant
that produces iron metal. You are told that the new shipment of ore
coming in contains 56.3% Fe2O3. Your company
asks you: how many tonnes of iron can be obtained from 5.00 x
102 tonnes of ore? (1 tonne = 1000 kg).
Molar masses: Fe 55.85 g / mol;
Fe2O3 159.7 g / mol
Analysis. You are given the amount of ore that
has to be processed. That will be your starting point for this
question. Once again, you'll need to work through moles. You'll also
have to turn "56.3% Fe2O3" into a conversion
factor:
56.3 % Fe2O3 = 56.3 g
Fe2O3 / 100 g ore
The unit path is then
mass of ore ---> mass of Fe2O3
---> moles Fe2O3 ---> moles Fe --->
mass Fe
So we begin with the mass of ore (5.00 x 102 tonnes)
and proceed in serval steps:
Step 1: mass of ore to mass of
Fe2O3 in grams
Step 2: mass of Fe2O3 to mass of Fe
Step 3: mass of Fe in grams to mass in tonnes
Step 1:
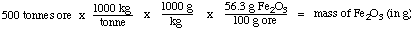
Step 2:
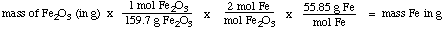
Step 3:
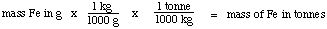
Summary
Learning this method takes practice, but it helps if you remember
the basic process:
- Write down what you are GIVEN and its units
- Write down what you are ASKED TO FIND and its units
- Determine the conversion factors that might be needed to
develop the units path beteween what you are given and what you
are asked to find.
- Finally, multiply what you are given by the conversion factors
(or their reciprocals if necessary to make the units cancel). If
the units of your final answer are correct, and your conversion
factors are correct, the answer you obtain almost certainly has to
be the correct answer.
HELPFUL HINTS:
- In the Dimensional Analysis Tutorial that you did in the first
lab, the conversion factors were referred to as "fractions"
(because they are fractions: one number with its units over
another number with its units).
- In Section 1 of the Tutorial, "Translation of Statements into
Fractions," you are asked to write the fraction in two ways. These
two ways correspond to the conversion factor and its reciprocal.
Back
to Lab Schedule
Back
to CHEM 1P80 Home Page
This page is
http://chemiris.labs.brocku.ca/~chemweb/courses/chem180/Dimensional_Analysis.html
Created October 10, 2000 by M. F. Richardson
© Brock University, 2000