Lecture 10
Chemical Equations and Stoichiometry
A. The meaning of a balanced chemical equation
A chemical equation is said to be balanced when there
are the same numbers of each atom on the left side (the reactants) as
on the right side (products). This is a consequence of the Law of
Conservation of Matter: matter can neither be created nor
destroyed. The equation is a "recipe" that tells you exactly how much
of each ingredient you have to use in order to get the product.
B. Two important types of reactions
There are many ways to classify chemical reactions.
For simplicity, let's just consider two of them now. These are
combination reactions and combustion reactions.
- Combination reactions. A combination reaction is said
to occur when two or more elements or compounds combine to produce
a third compound. Here are a few examples. (The equations are
balanced)
- Hydrogen reacts with oxygen to produce water:
- Magnesium reacts with fluorine to produce magnesium
fluoride:
- Sulfur dioxide reacts with oxygen to produce sulfur
trioxide:
- Combustion of organic compounds. Combustion occurs when
an organic (carbon-containing compound combines with oxygen in the
air to produce heat, flames, and the compounds carbon dioxide and
water. (Other substances may be produced if the original compound
contains elements other than C, H, and O.) For example,
- Methane (natural gas, CH4) burns in air to
produce water and carbon dioxide:
CH4 + 2 O2 ---> CO2 + 2
H2O
- Ethanol also burns in air to produce water and carbon
dioxide:
CH3CH2OH + 3 O2 ---> 2
CO2 + 3 H2O
- Methyl sulfide burns in air to produce not only water and
carbon dioxide, but also sulfur dioxide:
CH3SH + 3 O2 ---> CO2 +
2 H2O + SO2
C. Balancing Equations
Note that in each of the equations in part B, the
number and type of atoms on the left-hand side of the equation is
equal to the number and type on the right hand side. This is what
it means to have a balanced equation.
For example, in the combustion of ethanol:
CH3CH2OH + 3 O2
---> 2 CO2 + 3 H2O
On the left we have one molecule of ethanol
(CH3CH2OH) and 3 molecules of oxygen
(O2). On the right we have two molecules of carbon dioxide
(CO2) and three molecules of water (H2O). So
let's count atoms:
Left hand side: 2 C + 6 H + 1 O from ethanol, 6 O from
3 oxygen molecules
= 2 C + 6 H + 7 O
Right-hand side: 2 C + 4 O from two carbon dioxide molecules, 6 H
and 3 O from 3 water molecules
= 2 C + 6 H + 7 O
The coefficients in a balanced equation are called the
stoichiometric coefficients.
Many combination reactions can be balanced "by inspection." For
example, white phosphorus (P4) reacts with fluorine
(F2) to give PF5. We can express this reaction
by means of the "skeleton equation" (unbalanced) that just shows the
reactants and the products without the correct numbers of each.
P4 + F2 ---> PF5
(not balanced)
It is clear that one P4 molecule can produce 4
molecules of PF5. But if we have 4 molecules of
PF5, we need 20 F atoms, or 10 F2 molecules.
Thus the balanced equation is
P4 + 10 F2 ---> 4
PF5 (balanced)
The rules for balancing combustion reactions are given in
Kotz and Treichel, pp. 151-153 (4th ed.)
D. Use of the Balanced Equation: A Simple Example
Let's suppose I want to make sandwiches, each
consisting of 2 slices of bread (Bd) and 3 slices of turkey (Tk). My
"balanced equation" tells me how to make one sandwich:
2 Bd + 3 Tk ---> Bd2Tk3
Now, if I want to make 200 of these Bd2Tk3
sandwiches, how much Bd and Tk do I need?
200 Bd2Tk3 x 2 Bd / 1
Bd2Tk3 = 400 Bd
200 Bd2Tk3 x 3 Tk / 1 Bd2Tk3
= 600 Tk
However, Bd is sold in loaves that have 20 Bd/loaf, and Tk comes
in packages that have 8 slices/pkg. So I need to buy these
quantities:
400 Bd x 1 loaf / 20 Bd = 20 loaves of Bd
600 Tk x 1 pkg / 8 Tk = 75 pkg Tk
E. Use of the Balanced Equation: A Chemical Example
The anticancer drug cis-platin has the composition
Pt(NH3)2Cl2. It is made by the
following reaction:
(NH4)2PtCl4 + 2
NH3 ---> Pt(NH3)2Cl2 +
2 NH4Cl
This equation tells me that if I want to make a single
Pt(NH3)2Cl2 molecule, I need to take
one formula unit of (NH4)2PtCl4 and
2 molecules of NH3. (This is like making a single
sandwich). But I want to make enough to be useful for a cancer
patient, so I'm likely to need not one molecule, but 6.022 x
1023 molecules (1 mole!) Thus I would need 6.022 x
1023 units of (NH4)2PtCl4
(1 mole) and 2 x 6.022 x 1023 molecules (2 moles) of
NH3.
Just as in our sandwich analogy in part D, we have to consider the
"packaging" of our reactants. We don't count individual molecules, we
count by weighing. The formula weights (molar masses) of our
reactants and product are:
(NH4)2PtCl4 372.97
g/mol
NH3 17.03 g/mol
Pt(NH3)2Cl2 300.05 g/mol
So if I want to make one mole (300.05 g) of cis-platin, I will
need one mole (372.97 g) of
(NH4)2PtCl4 and two moles of
NH3 (34.06 g).
F. Stoichiometric Factors
Look at the equation for preparing cis-platin again:
(NH4)2PtCl4 + 2
NH3 ---> Pt(NH3)2Cl2 +
2 NH4Cl
The ratio of the stoichiometric coefficients, 2 mol NH3
/ mol (NH4)2PtCl4, is called the
stoichiometric ratio or stoichiometric factor for this
particular reaction. Other stoichiometric factors for this reaction
are:
2 mol NH3 / mol
Pt(NH3)2Cl2
2 mol NH3 / 2 mol NH4Cl
and so on...
Example: Suppose we want to make 100.0 g
Pt(NH3)2Cl2. What mass of
NH3 will be required?
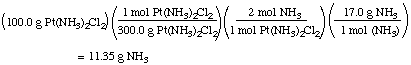
Notice that we used the stoichiometric factor 2 mol NH3
/ mol Pt(NH3)2Cl2 to solve this
problem, after first converting the mass of
Pt(NH3)2Cl2 to moles.
Back
to Lecture Schedule
Back
to CHEM 1P80 Home Page
This page is
http://chemiris.labs.brocku.ca/~chemweb/courses/chem180/CHEM1P80_Lecture_10.html
Created September 11, 2000 by M. F. Richardson
© Brock University, 2000