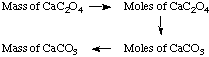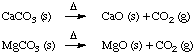Lecture 12

Chemical Analysis

A. Analysis of Mixtures When Only a Single Component Reacts with the Reagent

Drug stores sell various mineral supplements. One of these is a calcium-containing tablet, which contains powdered calcium carbonate as the active ingredient. There is also an inert "binder" that holds the calcium carbonate in its tablet shape. Thus the tablet is a mixture of substances, only one of which is important in a nutritional sense.

Let's suppose we want to analyze the tablet for its content of CaCO₃. We weigh the tablet, then add it to hydrochloric acid so that the calcium carbonate will dissolve:

CaCO₃ (s) + 2 HCl (aq) ---> CaCl₂ (aq) + H₂O (l) + CO₂ (g)

We filter the solution to remove any insoluble material. Then, to the filtered solution we add a solution of sodium oxalate in order to precipitate the insoluble compound, calcium oxalate (CaC₂O₄).

CaCl₂ (aq) + Na₂C₂O₄ (aq) ---> 2 NaCl (aq) + CaC₂O₄ (s)

We filter off the CaC₂O₄, dry it, and weigh it.

Numerical Example. Suppose that a calcium-supplement tablet weighs 1.250 g. After you carry out the above procedure, you obtain 1.508 g of dry CaC₂O₄. What percentage of the tablet is CaCO₃?

Solution. We will need to do mole/mass conversions, and use the stoichiometric factors that relate moles of calcium carbonate to moles of calcium oxalate, as depicted in the following scheme:

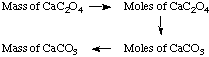
(1.508 g CaC₂O₄) x (128.10 g CaC₂O₄/ mol CaC₂O₄) = 1.1772 x 10^-2 mol CaC₂O₄

1.1772 x 10^-2 mol CaC₂O₄ x (1 mol CaCO₃ / mol CaC₂O₄) = 1.1772 x 10^-2 mol CaCO₃

1.1772 x 10^-2 mol CaCO₃ x (100.09 g CaCO₃ / mol CaCO₃) = 1.1783 g CaCO₃

Thus the percent CaCO₃ in the calcium tablet is

% CaCO₃ = (1.1783 g CaCO₃ / 1.250 g tablet) x 100

= 94.26% CaCO₃

 

B. Analysis of Mixtures When Two Components React With the Reagent

Numerical Example. The rock that Brock sits on is dolomitic limestone, a mixture of both CaCO₃ and MgCO₃. Both carbonates decompose on heating:

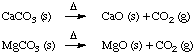
If 2.550 g of dolomite yields 1.341 g of MgO + CaO after heating, what is the % CaCO₃ in the dolomite? Report to 3 s.f.

Solution. Since we have two components, CaCO₃ and MgCO₃ , we might expect that we will have to use algebra in order to solve this problem. So let's think about what we know.

First, each mole of CaCO₃ that decomposes gives a mole of CO₂; similarly, each mole of MgCO₃ that decomposes also gives a mole of CO₂. Thus the total number of moles of CO₂ is equal to the moles of MgCO₃ plus the moles of CaCO₃:

Moles CO₂ = moles MgCO₃ + moles CaCO₃

The mass of CO₂ released on heating is

2.550 g dolomite - 1.341 g of MgO + CaO = 1.209 g CO₂

We now find moles of CO₂:

(1.209 g CO₂ ) x (1 mol CO₂ / 44.01 g CO₂ ) = 0.27471 mol CO₂ (1 extra s.f.)

Thus we now know that

0.27471 mol CO₂ = moles MgCO₃ + moles CaCO₃ (Eq. 1)

Now we have one equation but it contains two unknowns. So we have to get a second relationship between our unknowns. We are told at the beginning of this example that dolomite is a mixture of CaCO₃ and MgCO₃.So we know that

mass dolomite = 2.550 g = mass MgCO₃ + mass CaCO₃

Now we have another equation, also containing two unknowns. But we know how to interconvert masses to moles, so let's do it. So let x = mass CaCO₃(in g). Then

2.550 g = x g + mass MgCO₃

mass MgCO₃ (in g) = 2.550 g - x

Now we get the moles of calcium and magnesium carbonates:

mol CaCO₃ = (x g CaCO₃) x (1 mol CaCO₃ / 100.09 g)

mol MgCO₃ = (2.550 g - x g) x (1 mol MgCO₃ / 84.31 g)

Substituting these into Eq. 1 above,

0.27471 = x / 100.09 + (2.550 - x) / 84.31 (Eq. 2)

Solving Eq. 2, we find that

x = 1.484 g CaCO₃

And the percentage of CaCO₃ is

% CaCO₃ = (1.484 g CaCO₃ / 2.550 g dolomite) x 100

= 58.2%

 

C. Combustion Analysis of Organic Compounds

Organic compounds containing only the elements C, H, and O burn in air (or in O₂) to give CO₂ and H₂O as products. If the compound is burned in a combustion apparatus (Fig. 4.12 in Kotz and Treichel), CO₂ and H₂O can be separated from each other and weighed. These data allow us to determine the empirical formula of the compound.

Numerical Example. Suppose 1.042 g of an organic compound containing C, H, and O is subjected to combustion analysis, and yields 1.527 g CO₂ and 0.6250 g H₂O. What is the empirical formula?

Solution: We will be able to get the masses of carbon and of hydrogen from the masses of CO₂ and H₂O. However, the compound also contains oxygen. In order to get the mass of oxygen we will have to subtract the masses of carbon and hydrogen from the starting mass of the compound (1.042 g).

moles CO₂ = (1.527 g CO₂ ) x (1 mol CO₂/ 44.010 g CO₂)
= 3.470 x 10^-2 moles of CO₂

mass of C = 3.470 x 10^-2 moles of CO₂ x (1 mol C / mol CO₂) x (12.011 g C / mol C)
= 0.4168 g C

 

moles H₂O = (0.6250 g H₂O) x (1 mol H₂O / 18.015 g H₂O)
= 3.469 x 10^-2 moles of H₂O

mass of H = 3.469 x 10^-2 mol H₂O x (2 mol H / mol H₂O) x 1.0079 g H / mol H)
= 0.06993 g H

 

mass of O = 1.042 g of compound - mass C - mass O
= 1.042 g - 0.06993 g - 0.4168 g
= 0.5553 g O

Now that we have the masses of C, H, and O, we can determine the moles, and then the mole ratio that gives us the empirical formula.

moles C = (0.4168 g C) x (1 mol C / 12.011 g C) = 0.03470 mol C

moles H = (0.06993 g H) x (1 mol H / 1.0079 g H) = 0.06938 mol H

moles O = (0.5553 g O) x (1 mol O / 15.999 g O) = 0.03471 mol O

Divide by moles of C to get the mole ratios of H to C and O to C:

0.06938 mol H / 0.03470 mol C = 1.999 mol H / mol C

0.03471 mol O / 0.03470 mol C = 1.000 mol O / mol C

Hence, since there are two hydrogens and one oxygen for every carbon, the empirical formula is CH₂O.

This page is http://chemiris.labs.brocku.ca/~chemweb/courses/chem180/CHEM1P80_Lecture_12.html
Created October 5, 2000 by M. F. Richardson
© Brock University, 2000