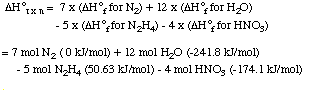Lecture 21
Hess's Law, State Functions, and Enthalpies of
Reaction
A. Hess's Law of Heat Summations
Hess's Law combines the law of conservation of energy
and the law of conservation of mass. It states: If a chemical
reaction (or process) can be expressed as a sum of separate
reactions, then the enthalpy change for the overall process is the
sum of the enthalpy changes for the constituent reactions.
Let's see how this applies to a reaction for which the enthalpy
change is experimentally unmeasureable: the production of gaseous
methane by the reaction of carbon (as graphite) with hydrogen gas:
C (s, graphite) + 2 H2 (g) --->
CH4 (g)
(NOTE 1: the reasons that the enthalpy change for this reaction
can't be measured experimentally are first, that the reaction is too
slow, and second, millions of compounds--the class of organic
compounds called the hydrocarbons--could be produced on the way to
methane.)
(NOTE 2: remember that carbon has more than one form that is
stable in the solid state. Diamond and graphite are the two best
known, but buckminsterfullerenes and nanotubes add to the list.
Different solid forms of a given element are called allotropes --
refer to Chapter 2 in Kotz and Treichel.)
There are other reactions whose enthalpy changes can be easily
determined, and if summed properly, the chemical equations add to
give the reaction above. A set of reactions which meet this
specification are:
|
Chemical Equation
|
|
|
1. C(s) + O2 (g) ---> CO2
(g)
|
-393.5
|
|
2. H2 (g) + 1/2 O2 (g)
---> H2O (l)
|
-285.8
|
|
3. CH4 (g) + 2 O2 (g)
---> CO2 (g) + 2 H2O (l)
|
-890.3
|
In order to decide how to use these, it is important to remember
that we want methane on the right-hand side, and graphite and
hydrogen gas on the left-hand side. We also want all reactants and
products other than C (s), H2 (g), and CH4 (g)
to cancel. It is clear that we will have to reverse the direction of
Equation 3 to get methane as a product, and that we will need
to take double the amounts in Equation 2 to cancel the water
in 1.
|
Chemical Equation
|

|
|
reverse 3: CO2 (g) + 2 H2O
(l) ---> CH4 (g) + 2 O2 (g)
1: C(s) + O2 (g) ---> CO2
(g)
double 2: 2 H2 (g) + O2 (g)
---> 2 H2O (l)
|
890.3
-393.5
-571.6
|
|
Overall: add the above reactions and cancel like terms on
both sides of the chemical equation to get the desired
equation.
C(s) + 2 H2 (g) --->
CH4 (g)
|
Add the above enthalpy changes to get the overall
enthalpy change for the desired reaction:
-74.8 kJ
|
Now we have determined that the enthalpy change for the reaction,
C(s) + 2 H2 (g) ---> CH4 (g), is -74.8 kJ
This process can be shown graphically. From equations 1
and 2 above, we find that a mole of carbon, two moles of
hydrogen, and two moles of oxygen combine to form a mole of carbon
dioxide and two moles of water to release 965.1 kJ of energy. Then we
imagine that the carbon dioxide and water thus formed react to
produce a mole of methane and two moles of oxygen, absorbing 890.3 kJ
of energy when they do so. The net energy change must be the
difference between these two processes, or 74.8 kJ of energy released
when methane is formed from the elements carbon and hydrogen.
B. State Functions
A state function is a quantity whose value is
determined only by the state of the system. State functions are
path-independent: you can't tell how you got there by looking
at where you are. Examples: You can't tell from looking at someone's
bank balance how it was achieved. You can't tell by looking at a
blown-up balloon whether it was blown up slowly or rapidly. For state
functions, only the initial and final values are important, not the
process used to get from the initial to the final state.
The enthalpy change (Delta H) and the overall energy change (Delta
E) are examples of state functions.
A practical example of state functions. Remember that
changes in the internal energy E are due to changes in the heat
evolved (or absorbed) and to work done by (or on) the system.
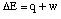
Now consider the burning of gasoline, represented as
the compound octane, C8H18:
2 C8H18 + 25 O2 --->
16 CO2 + 18 H2O
In the first case, we can burn the gasoline out in the open, in
which case almost all the energy from the reaction is released as
heat (there is a very small work term due to the volume change and
the PV work). Or we can burn the gasoline in an automobile engine and
harness a significant amount of the energy produced as mechanical
energy, that is used to turn the wheels of the car and propel it from
one destination to another.
The total energy change is divided differently in these two cases:
the work terms w have different values, and the heat terms q have
different values. Thus q and w are NOT state functions, even though
the internal energy and enthalpy changes ARE state functions.
C. Standard Enthalpies of Formation
When a reaction occurs with all reactants and products
in their standard states under standard conditions, the enthalpy
change is called the standard enthalpy change for the
reaction.
The standard state of an element or compound is the most
stable form of the element or compound in the physical state in which
it exists at 1 bar (100 kPa; 101.3 kPa = 1 atm) and a specific
temperature, usually 25o C.
The standard molar enthalpy of formation is the enthalpy
change that results when one mole of the compound is produced
directly from its elements, all in their standard states.

Some compounds and their standard molar enthalpies of formation
are shown in the table below. The reactions may have fractional
coefficients for the elements: the key is to take just enough to
produce one mole of the product.
|
Compound name
|
Formation reaction
|
f.gif)
|
|
Gaseous water, H2O (g)
|
H2 (g) + 1/2 O2 (g) --->
H2O (g)
|
-241.8
|
|
Liquid water, H2O (l)
|
H2 (g) + 1/2 O2 (g) --->
H2O (l)
|
-285.8
|
|
Hydrogen sulfide, H2S (g)
|
1/8 S8 (s, rhombic) + H2
(g) ---> H2S (g)
|
-20.63
|
|
Hydrazine, N2H4 (l)
|
N2 (g) + 2 H2 (g) --->
N2H4 (l)
|
50.63
|
When most chemical compounds form from their elements,
energy is released. The formation reaction is thus exothermic, and
the sign of the standard enthalpy of formation is negative. However,
there are some compounds whose formation is endothermic. Hydrazine is
such an example: hydrazine is unstable with respect to decomposition
back to its elements.
NOTE CAREFULLY: The units of kJ are understood to be "kJ/mol of
product" because of the way the standard enthalpy of formation is
defined.
D. Calculating Enthalpies of Reaction From Standard Enthalpies
of Formation
Let's consider one of the early rocket fuels. Liquid
hydrazine was stored in one set of fuel tanks, nitric acid in others.
These two compounds react vigorously with each other, producing large
volumes of gases (nitrogen and steam) along with much energy. The
overall reaction is
5 N2H4 (l) + 4 HNO3 (l)
---> 7 N2 (g) + 12 H2O (g)
We can imagine this reaction occurring in a series of 3 steps.
These 3 steps sum to the overall reaction in the last line of the
table, with an energy enthalpy that is equal to the sum of the
enthalpy changes for the three steps.
|
Reactions
|

|
|
1. Hydrazine decomposes to its elements.
5 N2H4 ---> 5
N2 + 10 H2
|
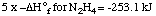
|
|
2. Nitric acid decomposes to its elements.
4 HNO3 ---> 2 H2 + 2
N2 + 6 O2
|

|
|
3. The hydrogen and oxygen produced in the previous
reactions combine to form water.
12 H2 + 6 O2 ---> 12
H2O
|
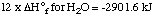
|
|
Sum of the above three equations:
5 N2H4 + 4 HNO3
---> 7 N2 + 12 H2O
|
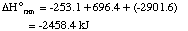
|
This set of steps can also be shown graphically:
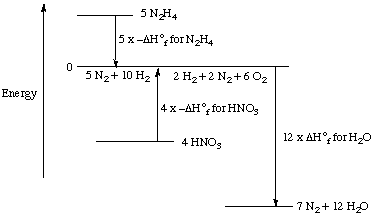
If you followed this reasoning carefully, you will
realize that the enthalpy change for the reaction was calculated from
the standard enthalpies of formation for each of the compounds:
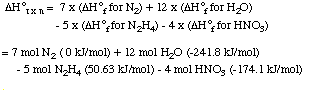
This leads to a general method for calculating the standard
enthalpy change for any reaction:
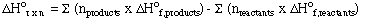
Back
to Lecture Schedule
Back
to CHEM 1P80 Home Page
This page is
http://chemiris.labs.brocku.ca/~chemweb/courses/chem180/CHEM1P80_Lecture_21.html
Created October 30, 2000 by M. F. Richardson
© Brock University, 2000