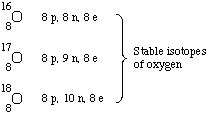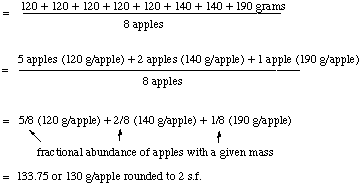Lecture 5

 Atoms, Isotopes, Atomic Weights

A. Atomic Composition; Isotopes

The nucleus is made up of protons and neutrons. The protons determine the chemical identity of the element (because the number of electrons in a neutral atom is equal to the number of protons, and it's the electrons that are responsible for the chemistry of an element).

The atomic number of an atom is the number of protons in its nucleus, and is written as a left subscript. The mass number is the number of protons plus the number of neutrons, and is written as a left superscript. The element symbol can be obtained from the atomic number or vice versa from the periodic table.

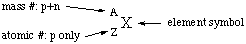
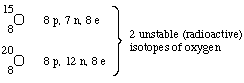
Isotopes are atoms which have the same atomic number but different mass numbers. Thus they are atoms of the same element whose masses are different because the number of neutrons is different. Some isotopes are radioactive, some are not. For example, oxygen has 3 naturally occurring, nonradioactive isotopes and several radioactive isotopes that are not found naturally.

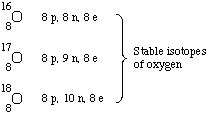
B. The Mass Spectrometer

In a mass spectrometer (Fig. 2.11, Kotz and Treichel), a gaseous sample is introduced into an ionization chamber. An electric discharge (the "electron gun") bombards the sample with electrons and causes ionization to occur. Positive ions are accelerated towards a detector, but their path is controlled by a magnetic field that allows only ions of a particular mass to reach the detector at a given time. Variation of the magnetic field results in all ions reaching the detector but at different times, thus resulting in a mass spectrum in which ions of different masses appear at different places on the chart.

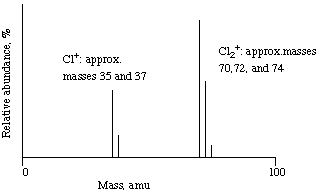
Below is a schematic mass spectrum for chlorine gas. The electrons from the electron gun strike the Cl₂ molecules, resulting in two processes occurring:

Process 1: An electron is knocked off of a Cl₂ molecule, resulting in Cl₂⁺ ions:

Cl₂ + e ---> Cl₂⁺ + 2 e

Process 2: The incoming electron breaks the Cl₂ molecule apart:

Cl₂ + e ---> Cl + Cl⁺ + 2 e

The positive ions (Cl₂⁺ and Cl⁺) are accelerated towards the detector, where their relative abundances are recorded. The mass spectrum shows two clusters of peaks: one cluster consists of two peaks, at masses of about 35 and 37, and the other cluster has three peaks, at masses of 70, 72, and 74.

The appearance of two peaks at masses 35 and 37 shows that chlorine has two stable isotopes. The three peaks at masses 70, 72, and 74 are due to the combinations of two ³⁵Cl atoms, one ³⁵Cl and one ³⁷Cl, and two ³⁷Cl atoms, respectively.

C. Exact Determination of Atomic Masses from the Mass Spectrum

Very accurate measurements can be made by means of a mass spectrum. The peak cluster that is due to Cl⁺ can be analyzed as follows:

Peak at mass 35 (approx.): exact mass is 34.96885 amu; 75.77% of the total Cl⁺ cluster.

Peak at mass 35 (approx.): exact mass is 36.96590 amu; 24.23% of the total Cl⁺ cluster.

(1 amu = 1/12 of the mass of an atom of ¹²C)

The atomic weight of chlorine is the average mass of a chlorine atom. We will calculate the atomic weight for chlorine in Section E below.

 

D. Calculation of Average Mass

Before we calculate the atomic weight of chlorine, let's consider a simpler example. Suppose I buy a basket of 8 apples. I weigh each one and find the following results

• 5 apples each have a mass of 120 g
• 2 apples each have a mass of 140 g
• 1 apple weighs 190 g

Now to get the average mass, I add up all the individual masses and divide by the number of apples. But let's show how this relates to fractional or percentage abundances, so we have a closer relationship to the data from the mass spectrum of chlorine. Thus,

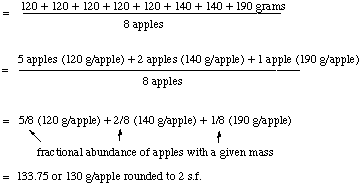
Note that we have derived a very simple way to calculate the average mass when we know the percentage or fractional abundance of each object with a given mass. (Remember that % = fractional abundance * 100).

Average mass = (fraction of A)*(mass of A) + (fraction of B)*(mass of B) + ...

 

E. The Atomic Weight of an Element

Now we know the atomic masses for atoms of each of the two chlorine isotopes. The atomic weight of an element is the average mass of an atom of that element. The average is taken over a large number of atoms: each peak in a mass spectrum is due to millions of ions.

Let's use the data in Section C above to calculate the atomic weight of chlorine.

75.77 % ³⁵Cl = 0.7577 fractional abundance
24.23% ³⁷Cl = 0.2423 fractional abundance

Thus, since the average mass of a chlorine atom equals the atomic weight of chlorine,

Atomic weight of chlorine = 0.7577 * 34.96885 amu/atom + 0.2423 * 36.96590 amu/atom

= 35.45 amu/atom

 

This page is http://chemiris.labs.brocku.ca/~chemweb/courses/chem180/CHEM1P80_Lecture_5.html
Last modified September 20, 2000 by M. F. Richardson
© Brock University, 2000