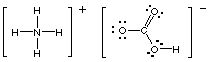
1. Hint #1. As a general rule for binary compounds, covalent compounds are formed when a nonmetal reacts with another nonmetal or with a metalloid, and ionic compounds are formed when a metal reacts with a nonmetal.

Hint #2. For compounds that contain several elements, it is extremely helpful if you remember the formulas of cations and anions that contain nonmetals. For example, the acetate ion is CH₃CO₂^- and so NaCH₃CO₂ is an ionic compound (though the anion contains covalent bonds). Similarly, NH₄HCO₃ is an ionic compound because it contains the ammonium cation and the bicarbonate anion. There is covalent bonding within each ion, but the ions are not covalently bonded to each other: the compound forms because of electrostatic attractions between the oppositely charged ions.

Hint #3. The Lewis structure of ammonium bicarbonate shows why the compound has to be ionic: The nitrogen has an octet of electrons about it, and no lone pairs, so it cannot be involved in covalent bonding to any other atom.

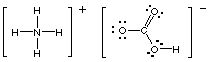
2. Hints and Worked Example. The key to this question is to recognize the relationship between ionic bond length, lattice energy, and melting point.

Coulomb's Law states that the energy of attraction between oppositely charged ions depends inversely on the distance and directly on the product of the charges of the anion and cation. Thus the shorter the distance (if ion charges are the same), the stronger the attractive forces and the greater the lattice energy. The higher the ion charges (if distances are equal), the greater the lattice energy.

In order to melt an ionic compound, the attractive forces between the ions (which hold the solid in its rigid shape) must be overcome by the energy supplied as heat. The less attraction between the ions, the less heat will have to be supplied, and the lower the melting point.

Example. Consider the compounds CdI₂, ZnCl₂, and CdBr₂. Which has the shortest bonds? Which has the highest lattice energy? Which has the lowest melting point?

Solution. From periodic trends, Cd²⁺ is expected to be larger than Zn²⁺. Of the three halide ions in this series, iodide is the largest and chloride is the smallest. Thus ZnCl₂ has the smallest cation and smallest anion, thus has the shortest bonds and the highest lattice energy. The lowest-melting compound will be the one with the lowest lattice energy (longest bonds), which is CdI₂.

Solution. The covalent radii of the halogens follow the same trend as the ionic radii of the halide ions. Just as iodide has the largest ionic radius and fluoride the smallest in the series F^-, Cl^-, Br^-, and I^-, iodine has the largest and fluorine the smallest covalent radius. Thus SbI₃ has the longest bonds and SbF₃ the shortest.

Antimony has an electronegativity of 1.9, whereas the electronegativities of F, Cl, Br, and I are 4.0, 3.0, 2.8, and 2.5, respectively. Thus SbF₃ has the most polar bonds and SbI₃ the least polar bonds.

Solution. Draw the Lewis structures of all the molecules. You should have only one that has no lone pairs on the central atom.

                

          

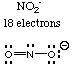
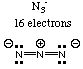
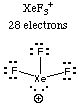
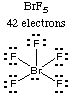
The only structure with no lone pairs on the central atom is the azide ion, N₃^-. (Sodium azide is the compound used in automobile air bags; it decomposes rapidly in the event of a collision to release gaseous nitrogen, which inflates the bag.)

6. Example. Consider the molecules and ions whose Lewis structures were drawn in Question 4 and whose molecular and electron-pair geometries were given in Question 5.

(a) Which one has only bond angles of 109.5 degrees? Answer: only molecules with a tetrahedral distribution of electron pairs about the central atom can have this angle. Therefore SOCl₂.

(b) Which one has only bond angles of 120 degrees? Answer: only molecules with triangular planar electron pair geometries have angles of 120 degrees and no other value. Therefore NO₂^-.

(c) Which one has only 180 degree bond angles? Answer: only linear molecules can have a 180-degree bond angle. N₃^-.

(d) Which one has exactly two bond angles of 90 degrees? Answer: Both XeF₃⁺ and BrF₅ have molecular geometries with 90-degree bond angles. BrF₅ has eight angles equal to 90 degrees, but XeF₃⁺ has only two angles equal to 90 degrees. Therefore XeF₃⁺. (Sketch the shapes to see that this is so.)
 
 

7. Hints and Example. Which one of the following molecules is nonpolar? COCl₂, BrF₅, PF₅.

The Lewis structure for BrF₅ is drawn in Question 4 and its geometry is described in Question 5. The bond dipoles of the four Br-F bonds in the square plane (the square pyramid base) cancel each other, but the 5th Br-F bond (from the Br in the square pyramid base to the apex of the pyramid) has a dipole that is not cancelled by any other bonds.

The Lewis structure for COCl₂ is shown below. The molecule is planar but has a dipole moment because the bond dipoles don't cancel the C=O bond dipole (p. 425 Kotz and Treichel).

The Lewis structure for PF₅ (below) shows that the expected molecular structure is trigonal bipyramidal. The three P-F bonds in the triangular plane have bond dipoles that cancel each other, as do the axial P-F bonds. Thus PF₅ is the nonpolar molecule.

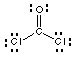
This page is http://chemiris.labs.brocku.ca/~chemweb/courses/chem180/CHEM_1P80_Assign_11.html
Last revised: August 20 2000 by M. F. Richardson
© Brock University, 1999