![]()
1. Hints. The mass number A of an element whose symbol is X is the sum of the number of neutrons and number of protons. The atomic number Z is the number of protons in the nucleus.
![]()
Remember that a neutral atom has no charge, hence the number of electrons is equal to the number of protons.
When you know the atomic number, you can use the periodic table to find
the element.
2. Sample question. The mass spectrum of the isotopes of silicon is shown below.
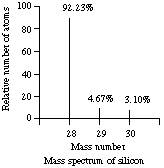
(a) How many protons are there in an atom of the most abundant isotope? (b) How many neutrons are there in an atom of the most abundant isotope? (c) How many electrons are there in an atom in the most abundant isotope?
Hint for (a)-(c): You know what the element is, so you know its atomic number and the number of electrons. See Example 2.3, p. 76 in Kotz and Treichel 4th ed.
(d) If the masses of the three isotopes are 27.9769 amu, 28.9765 amu, and 29.9738 amu, calculate the atomic weight of silicon and report it to the correct number of significant figures.
Solution to (d): The atomic mass of an element is the average of the masses of all the isotopes in a representative sample.
Average mass of silicon = 0.9223*27.9769 + 0.0467*28.9765 + 0.0310*29.9738
3. Sample Question. In this question you will show how the law of multiple proportions applies to two compounds made up of iodine and fluorine.= 25.80309 + 1.35320 + 0.92919 (correct s.f. in red)= 28.08549 = 28.09 properly rounded to 2 decimal places
One gram of Compound 1 contains 0.6902 g of I and 0.3098 g of F. One gram of Compound 2 contains 0.4883 g of I and 0.5117 g of F.
From data like this, Dalton deduced that the I/F ratios of the numbers of the atoms in the two compounds were the same as the I/F ratios of the masses in the two compounds. Today, we know these two compounds are IF3 and IF7. (Note the 7:3 ratio of the fluorines).(a) What is the I/F ratio in Compound 1? Ans. 0.6902/0.3098 = 2.227(b) What is the I/F ratio in Compound 2? Ans. 0.4883/0.5117 = 0.9543
(c) Divide the I/F ratio for Compound 1 by the I/F ratio for Compound 2. Report your answer as a ratio of small whole numbers. Ans. 2.227/0.9543 = 2.334 which, in small whole numbers is 7:3
4. Hint. Information needed for this question is in the text,
the Figures, and the Tables of section 2.8 of Kotz and Treichel, 4th ed.
5. Sample problem. The data in the table below were collected in a Millikan oil drop experiment.
(a) Calculate the average charge on an electron (in Coulombs).
(b) How many electrons have accumulated on each oil drop?
(c) The accepted value of the electron charge is 1.602 x 10-19 C. Calculate the % error or your answer in part (a)
Solution. Each oil drop has to have a whole number of electrons on it. It's probably easiest to do part (b) first, i.e. divide the measured charge by the accepted charge on a single electron ( 1.602 x 10-19 C) and round to the nearest whole number. Thus oil drops 1, 2, 3, 4, and 5 have 2, 5, 3, 7, and 1 electrons respectively.
Now that you know the number of electrons per drop, you can calculate the average charge on an electron in each drop.
The average is thus [(1.6025 + 1.6030 + 1.6023 + 1.6043 + 1.6030) x 10-19]/5 = 1.603 x 10-19 Coulombs per electron.
Oil Drop # Average Charge (C) per electron on this drop
(c) The % error is 100 x [(1.603 - 1.602) x 10-19]/(1.602
x 10-19) = 0.06%. (see Chapter 1, p. 44)
This page is http://chemiris.labs.brocku.ca/~chemweb/courses/chem180/CHEM_1P80_Assign_2.html
Last revised: August 20 2000 by M. F. Richardson
© Brock University, 1999