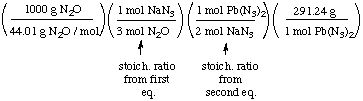Hints for Assignment 4
1. Sample Question. The elements iron and bromine react to give
iron(III) bromide according to the balanced equation
2 Fe + 3 Br2 ==> 2
FeBr3
Suppose you have 0.3942 mol of iron.
(a) How many moles of
Br2
are needed for complete reaction?
(b) What mass of FeBr3 can be produced?
(The molar mass of FeBr3 is 295.56 g/mol.)
Solution. The balanced equation gives you the
mole ratio for the reaction (3 moles of Br2 to 2 moles of Fe)
and for the product formed (2 moles of FeBr3 produced for each
two moles of Fe that react). By dimensional analysis:
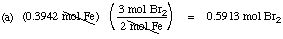
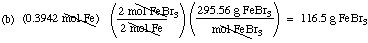
2. Sample Question. Scandium metal reacts with
dilute sulfuric acid according to the following unbalanced equation:
Sc (s) + H2SO4 (aq)
==> Sc2(SO4)3 (aq) + H2
(g)
Suppose you react 9.03 g of scandium metal with excess dilute sulfuric
acid.
(a) What mass of Sc2(SO4)3,
in grams, can be obtained?
(b) What mass of hydrogen gas, in grams, can be obtained?
(c) If only 32.4 g of Sc2(SO4)3
is obtained, what is the % yield of Sc2(SO4)3?
Solution Hints. Hint 1: First balance
the equation:
2 Sc (s) + 3 H2SO4 (aq)
==> Sc2(SO4)3
(aq) + 3 H2 (g)
Hint 2: The balanced equation relates moles
of reactants and moles of products. We have a mass and are asked for a
mass. Thus the sequence of operations for solving the problem is
mass Sc ==> moles Sc ==> molesSc2(SO4)3
==> mass Sc2(SO4)3
Solutions (by dimensional analysis)
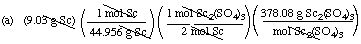
= 38.0 g
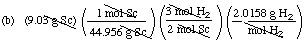
= 0.607 g
(c) Remember that the percent yield is
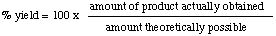
= 100 x 32.4 g obtained / 38.0 g possible
= 85.3 %
3. Sample Question An unknown element reacts
with oxygen to give the oxide, M2O5. If 1.854 g of
the element gives 3.310 g of the oxide, what is the element?
Analysis of the question: we know the mass
of the element and the mass of oxide that is obtained, so we can obtain
the mass of the oxygen, and calculate the moles of oxygen atoms present.
We know the mole ratio of oxygen to the element (5:2) from the formula
given, so we will be able to calculate the moles of element. The molar
mass (and thus the atomic weight) of the element can then be calculated
from the mass and moles.
Mass oxygen = 3.310 g oxide - 1.854 g element
= 1.456 g oxygen
Moles of oxygen atoms = (1.456 g oxygen) x (1 mol
O / 16.00 g)
= 0.09100 mol O
Therefore, moles of M atoms = (0.09100 mol O) x (2 mol
M / 5 mol O)
= 0.03640 mol M
The molar mass is
1.854 g M / 0.03640 mol M
= 50.93 g M /mol M
The element whose atomic weight is closest to 50.93
g/mol is vanadium, V.
4. Sample Question Fe2(SO4)3
reacts with sodium pyrophosphate, Na4P2O7,
according to the equation
2 Fe2(SO4)3
(aq) + 3 Na4P2O7 (aq) ==>
Fe4(P2O7)3 (s) + 6 Na2SO4
(aq)
(a) Which reactant is limiting if 4.456 g of Fe2(SO4)3
and
3.923 g of Na4P2O7 are allowed to react?
(b) What mass of Fe4(P2O7)3
can be produced?
(c) What mass of the excess reactant remains when
the reaction is complete?
Formula weights (g/mol): Fe2(SO4)3
399.881; Na4P2O7 265.903; Fe4(P2O7)3
745.213.
Solutions.
(a) We need to compare moles of Fe2(SO4)3
and
moles of Na4P2O7.
mol Fe2(SO4)3
=
(4.456 g) (1 mol / 399.881 g) = 0.01114 mol
mol Na4P2O7 = (3.923
g) (1 mol / 265.903 g) = 0.01475 mol
Now let's determine how much Na4P2O7
is needed to react with 0.01114 mol Fe2(SO4)3:
mol Na4P2O7
needed:
= 0.01114 mol Fe2(SO4)3
x (3 mol Na4P2O7 / 2 mol Fe2(SO4)3)
= 0.01671 mol Na4P2O7
We don't have this much Na4P2O7
so Na4P2O7 is the limiting reagent.
(b) Calculate mass of Fe4(P2O7)3
that can be produced from 0.01475 mol Na4P2O7:
0.01475 mol Na4P2O7
x (1 mol Fe4(P2O7)3 / 3 mol
Na4P2O7) x 745.21 g/mol
= 3.665 g Fe4(P2O7)3
(c) Amount of Fe2(SO4)3in
excess = initial amount - amount reacted.
Amount reacted:
= 0.01475 mol Na4P2O7
x (2 mol Fe2(SO4)3/3 mol Na4P2O7)
= 9.836 x 10-3
mol Fe2(SO4)3
We began with 0.01114 mol Fe2(SO4)3,
so the amount remaining (in grams) is
(0.01114 mol - 9.836 x 10-3 mol) x 399.881
g Fe2(SO4)3/mol
= 0.521 g
5. Hints for (a) and (b); Sample Question with hints
for part (c)
(a) and (b): See Example 4.2,
pp. 155-156 in 4th edition, Kotz and Treichel
(c). How many liters of air at 25°C are
required to roast 1.00 kg of silver sulfide? Assume that air contains 23%
O2 by mass and that the density of air at 25°C is 1.2 g/L.
The equation for the reaction is:
Ag2S + O2 ==> 2 Ag
+ SO2
Solution Hints for part (c). The sequence of
steps to solve this problem is:
moles Ag2S ==> moles O2
==>
mass
O2 ==>mass of air ==>volume of air
Note that "air contains 23% O2 by mass"
becomes
(0.23 g O2 / g air) or, equivalently,
(1 g air / 0.23 g O2)
The density of air (1.2 g/L) means that each liter of
air weighs 1.2 g, or that 1.2 g of air occupies a volume of one liter at
25°C.
6. Sample Question. A mixture of CaSO4
and its hydrate CaSO4.1/2H2O
has a mass of 5.4786 g. After heating to drive off all the water, the mass
is only 5.3114 g. What is the weight percentage of CaSO4.1/2H2O
in the original mixture?
Molar masses: CaSO4 136.14
g/mol; CaSO4.1/2H2O
145.15 g/mol
Analysis of the question. One of these compounds
contains water of hydration; the other does not. Therefore we will be able
to determine the amount of the hydrated compound from the mass of the water
that is lost on heating.
mass H2O lost = 5.4786 - 5.3114
g = 0.1672 g
moles CaSO4.1/2
H2O originally present
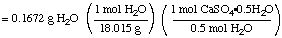
= 0.01856 mol CaSO4.1/2H2O
Now calculate the mass of CaSO4.1/2H2O
and find the percentage. (Ans. 49.18%)
7. Hint: See Example 4.5, p. 166-167 in Kotz
and Treichel, 4th ed.
8. Sample Question. Lead azide, Pb(N3)2,
is a popular detonator for commercial explosives, valued especially because
of its reliability in damp conditions. It is made in a two-step reaction.
First, sodium azide, NaN3, is prepared from nitrous oxide (dinitrogen
monoxide, N2O) and metallic sodium in liquid ammonia. Then the
sodium azide is allowed to react with lead nitrate in a metathesis reaction
to produce lead azide. The equations are:
3 N2O + 4 Na + NH3 ==>
NaN3
+ 3 NaOH + 2 N2
2 NaN3
+ Pb(NO3)2 ==>
Pb(N3)2
+ 2 NaNO3
What mass of Pb(N3)2 (in kg) can
be produced from 1.00 kg of nitrous oxide? Molar masses: Pb(N3)2
291.24 g/mol; N2O 44.01 g/mol
Solution. There are two reactions,
and the product of the first becomes a reactant in the second. Thus
we apply the stoichiometric ratios in succession.
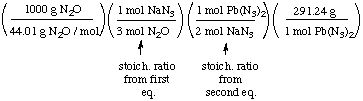
= 1102 g or 1.10 kg when properly
rounded and given in the units asked for.
9. Hint. See Example 4.7, pp. 170-171 in 4th
edition of Kotz and Treichel.
10. Sample Question. Both Na2SO4
and K2SO4 react with Ba(NO3)2
in aqueous solution to produce a precipitate of BaSO4, which
can be filtered and weighed. If 0.2784 g of a Na2SO4 -
K2SO4 mixture produces 0.4018 g of BaSO4,
what is the percentage of K2SO4 in the mixture? Report
your answer to 3 significant figures. HINT: There are two equations with
two unknowns.
Molar masses (g/mol): Na2SO4
142.044; K2SO4 174.261; BaSO4 233.391
Analysis of the problem. The BaSO4
produced tells us the total moles of Na2SO4 and K2SO4
present.
moles BaSO4 = moles K2SO4
+ moles Na2SO4 (equation 1)
We also know that the total mass is the sum of the masses
of Na2SO4 and K2SO4
mass Na2SO4 + mass
K2SO4 = total mass(equation 2)
Solution. Let x be the mass of K2SO4
(in grams). Then
mass Na2SO4 = 0.2784
g - x (from equation 2)
Now find moles of all compounds
moles K2SO4 = x g
K2SO4 /
(174.261 g K2SO4/mol)
moles Na2SO4 = (0.2784 - x)
g Na2SO4 / (142.044
g Na2SO4/mol)
moles BaSO4
= 0.4018 g BaSO4
/ (233.391 g BaSO4/mol)
Substitute these values into equation 1 and solve for
x
x = 0.1832 g K2SO4
Therefore the percentage of K2SO4 in
the mixture is
% K2SO4 = 100 x 0.1832
g / 0.2784 g = 65.8%
Back
to CHEM 180 Home Page
Back
to Assignment Schedule
This page is http://chemiris.labs.brocku.ca/~chemweb/courses/chem180/CHEM_1P80_Assign_4.html
Last revised: August 20 2000 by M. F. Richardson
© Brock University, 1999
![]()