Reaction
1. 2 CO (g) + O2 (g) ---> 2 CO2 (g)
-566.0
2. 2 H2 (g) + O2 (g) ---> 2 H2O (l)
-571.6
3. CH3CO2H (l) + 2 O2 (g) ---> 2 CO2 (g) + 2 H2O (l)
-874.5
Questions 1-4 are designed to give you some experience in answering multiple choice questions, as they form a part of your examinations in CHEM 1P80.
1. Hint. Review Figure 6.9 in Kotz and Treichel, or Question
9 on Assignment 7. Remember that the molar heat of fusion is the heat required
to convert one mole of a substance from a solid to a liquid at the melting
point, and the heat of vaporization is the heat required to convert one
mole of a substance from a liquid to vapor at the boiling point.
2. Hint. Get the heat capacity per mole (that's what the molar
heat capacity is) and decide which molar heat capacity is the highest and
which the lowest.
3. Hint. Sign conventions are important here.
4. Hint. If 1.000 g of a substance with a known molar mass produces a certain amount of energy, how do you calculate what amount of energy is produced by one mole of the substance?
Calculate the energy change for Step 1 and for Step 2, then add them to get the total energy change.
5. Example. Write the chemical equation for the standard molar enthalpy of formation of trimethylammonium perchlorate, (CH3)4NClO4
Remember that this equation will have one mole of compound on the right hand side of the equation. The left-hand side of the equation will contain the elements that make up the compound. The equation must be balanced.6. Example. The heat of reaction for the preparation of acetic acid from carbon monoxide and hydrogen gas cannot be measured directly but can be determined indirectly from other heats of reaction by applying Hess's Law. Given the following data for the combustion of carbon monoxide, hydrogen, and acetic acid in oxygen:This compound is made up of five elements: C, H, N, Cl, and O. The standard states of each of these can be found in Appendix L (the standard state of an element is the most stable form of the element in the physical state at which it exists at the specified temperature and 1 bar pressure).
Hydrogen, nitrogen, chlorine, and oxygen are diatomic molecular gases at 25 C and 1 bar pressure. Carbon is a solid under these conditions, and reference to Appendix L shows that graphite is the most stable form of the solid.
Thus the equation is:
4 C (s, graphite) + 6 H2 + 1/2 N2 + 1/2 Cl2 + 2 O2 ---> (CH3)4NClO4
Reaction |
|
1. 2 CO (g) + O2 (g) ---> 2 CO2 (g) |
-566.0 |
2. 2 H2 (g) + O2 (g) ---> 2 H2O (l) |
-571.6 |
3. CH3CO2H (l) + 2 O2 (g) ---> 2 CO2 (g) + 2 H2O (l) |
-874.5 |
Calculate the enthalpy of reaction for the preparation of acetic acid from carbon monoxide and hydrogen:
2 CO (g) + 2 H2 (g) ---> CH3CO2H (l)Solution: We want to write equations 1, 2, and 3 in such a way that they sum to give us the desired equation. Equation 1 has one of the reactants for the preparation of acetic acid (2 CO) on its left hand side, and Equation 2 has the second reactant for the preparation of acetic acid (2 H2) on its left hand side. We need to reverse equation 3, since acetic acid must be the product when carbon monoxide and hydrogen react. Thus:
Reaction |
|
1. 2 CO (g) + O2 (g) ---> 2 CO2 (g) |
-566.0 |
2. 2 H2 (g) + O2 (g) ---> 2 H2O (l) |
-571.6 |
3. (reversed; sign changes for the heat of reaction) |
+874.5 |
Sum the above 3 reactions, and add their heats: |
|
Thus, the enthalpy of reaction is -263.1 kJ (exothermic) for the preparation of acetic acid from carbon monoxide and hydrogen according to the equation7. Example. (a) Use data from Appendix L in the 4th edition of Kotz and Treichel, calculate the enthalpy change for the following reaction:2 CO (g) + 2 H2 (g) ---> CH3CO2H (l)
(b) List the data you use.NH4NO3 (s) ---> 2 H2O (g) + N2O (g)
Solution. We will use data for standard heats of formation to solve this problem (these are the answers to part (b):8. Worked example. Metallic aluminum reacts with hydrochloric acid according to the folowing equation:
The enthalpy for the reaction given in part (a) is
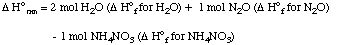
 = - 36.0 kJ
= - 36.0 kJ
The enthalpy change associated with this reaction can be determined with an ice calorimeter. If 20.2 g of ice are melted when 0.3581 g of Al reacts with excess hydrochloric acid, what is the enthalpy change (in kJ/mol Al) for the reaction written above? The heat of fusion of ice is 333 J/g.Al (s) + 3 HCl (aq) ---> AlCl3 (aq) + 3/2 H2 (g)
Solution. The heat generated from the reaction is absorbed by the ice so that some ice is converted to liquid water. Thus qreaction + qice = 0, or qreaction = - qice9. Worked example. A 2.625-g sample of caffeine, C8H10N4O2 (194.20 g/mol) was burned in a bomb calorimeter with excess oxygen. The temperature of the calorimeter and the water before combustion was 17.43 °C; after combustion the calorimeter and the water had a temperature of 20.48 °C. The calorimeter had a heat capacity of 832 J/K, and contained 0.874 kg of water. Use these data to calculate the molar heat of combustion (in kJ) of caffeine.qice = (20.2 g ice) x (333 J/g) = 6727 JNow 0.3581 g of Al is 0.013273 moles of Aluminum, so the enthalpy change isTherefore qreaction = - 6727 J (heat released by reaction of aluminum)
(- 6727 J / 0.013273 mol) x 1 kJ / 1000 J = - 507 kJ / mol Al
Solution. First let's find the heat gained by the calorimeter and the water.Now we know that combustion of 2.625 g caffeine produces 13.69 kJ of energy (combustion produces heat so this is exothermic; the signed value is -13.69 kJ).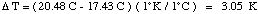
Heat gained by calorimeter = (832 J / K) x 3.05 K
= 2537.6 J = 2.538 kJ (1 extra s.f.)Heat gained by water = (874 g water) x (4.184 J/g-K) x (3.05 K)= 11,150 J = 11.15 kJ (1 extra s.f.)Total heat gain by calorimeter plus water = 13.69 kJ (still has 1 extra s.f.)Calculate the moles of caffeine:
moles caffeine = 2.625 g caffeine x (1 mol /194.20 g) = 0.013517 molesSo the molar heat of combustion is- 13.69 kJ / 0.013517 moles = 1013 kJ / mol= - 1.01 x 103 kJ /mol when rounded to the correct number of s.f.
This page is http://chemiris.labs.brocku.ca/~chemweb/courses/chem180/CHEM_1P80_Assign_8.html
Last revised: August 20 2000 by M. F. Richardson
© Brock University, 1999