Hints for Assignment 7, CHEM 1P81

Chemical Equilibrium


1. Example. Consider the following reaction:

2 NH3 (g) ---> N2 (g) + 3 H2 (g)

An experiment is carried out at a certain temperature; the starting concentration of NH3 is 0.300 mol/L. No products are present at the beginning of the reaction. When equilibrium is established, the concentration of N2 (g) is 0.130 mol/L. Calculate the equilibrium constant for the reaction.

Solution. The equilibrium constant expression is

We are given the starting and equilibrium concentrations of N2. If we assume a volume of exactly one liter, then the starting amount of the NH3 is 0.300 moles and the equilibrium amount of N2 is 0.130 moles.

Since 3 moles of H2 are produced for every mole of N2 produced, the equilibrium amount of H2 is

(0.130 mol N2) x (3 mol H2 / mol N2) = 0.390 mol H2

The equilibrium amount of NH3 is

moles NH3 at equilibrium = moles NH3 initially - moles NH3 reacted

Every mole of N2 that is produced results from the reaction of two moles of NH3 so that the amount of NH3 that reacted is

(0.130 mol N2) x (2 mol NH3 / mol N2) = 0.260 mol NH3

Thus,

moles NH3 at equilibrium = 0.300 moles NH3 initially - 0.260 moles NH3 reacted

= 0.040 moles NH3 at equilibrium

Since we chose to work with a volume of exactly one liter, [NH3] = 0.040 mol/L, [N2] = 0.130 mol/L, and [H2] = 0.390 mol/L. Substituting these values into the equilibrium constant expression, we find that the equilibrium constant KC = 4.75.

See also Section 16.4. The equilibrium table for the above reaction is shown below, where given data are shown in bold red type.

Equation 
2 NH3 --->
N2
+ 3 H2
Initial moles 
0.300
0
0
Change in moles 
- 0.260
0.130
0 + 0.390
Moles at equilibrium 
0.300 - 0.260 = 0.040
0 + 0.130 = 0.130
0 + 0.390 = 0.390
Concn. at equilibrium 
0.040 M
0.130 M
0.390 M

2. Ammonia decomposes to produce nitrogen and hydrogen according to the following reaction:

2 NH3 (g) ---> N2 (g) + 3 H2 (g)

Suppose that at some temperature (different from the temperature in Question 1), 6.48 moles of ammonia are placed in a reaction vessel whose volume is 30.0 liters. When equilibrium is established, it is found that 4.56 moles of ammonia remain. What is the equilibrium constant for the reaction at this temperature?

Solution. Let's set up an equilibrium table as done in Question 1. Given data are shown in bold red type.

Equation 
2 NH3 --->
N2
+ 3 H2
Initial moles 
6.48
0
0
Change in moles 
6.48 - 4.56 = 1.92
0.960
2.88
Moles at equilibrium 
4.56
0 + 0.960 = 0.960
0 + 2.88 = 2.88
Concn. at equilibrium 
=4.56 mol/30.0 L
= 0.152 M
0.960 mol/30.0 L
= 0.0320 M
2.88 mol/30.0 L
= 0.096 M

Thus the equilibrium constant for the reaction at this temperature is

= 0.00123


 
 

3. Example. Nitrogen and oxygen react to produce nitric oxide according to the following equation:

N2 (g) + O2 (g) ---> 2 NO (g)

The equilibrium constant for this reaction is 1.70 x 10-3. Suppose that 0.200 mol N2 and 0.400 mol O2 are mixed in a 2.00-L reaction vessel. What will be the concentrations of N2, O2, and NO when equilibrium is established? (Hint: assume that the amounts of N2 and O2 that react are small&emdash;less than 10% of the starting amounts&emdash;and check your assumption when you have solved the equation.)

Solution. Set up the Equilibrium Table.

Equation 
N2 +
O2 --->
2 NO
Initial concentration 
0.100
0.200
0
Change in concentration 
-x
-x
2x
Concn. at equilibrium 
0.100 - x
0.200 - x
0 + 2x

Write the equilibrium expression, and substitute the equilibrium concentrations in it. We will assume that x is a small percentage of the starting concentrations, which allows a simple solution to the problem. (See Example 16.8 in your text if you want to see the quadratic equation solved.

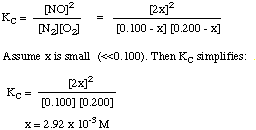
Since x is less than 10% of 0.100, we can avoid solving the quadratic equation. Thus our final concentrations are:

[N2] = 0.100 - 0.003 = 0.097 M

[O2] = 0.200 - 0.003 = 0.197 M

[NO] = 2 x 2.92 x 10-3 = 5.84 x 10-3 M

(If you solve the quadratic equation, you will find that x = 2.85 x 10-3 M.)
 
 

4. Hints. See Section 16.6 on LeChatelier's Principle, especially Table 16.2.
 
 

5. Hints. See Section 16.3 on The Reaction Quotient.
 
 

6. Hints. See Section 16.2 on The Equilibrium Constant. Example 16.1 gives an example of manipulating equilibrium constant expressions.
 
 

Back to Chem 1P81 Home Page

Back to Assignment Schedule
 

This page is http://chemiris.labs.brocku.ca/~chemweb/courses/chem181/CHEM_1P81_Assign_7.html
Last revised: March 3 2001by M. F. Richardson
© Brock University, 2001