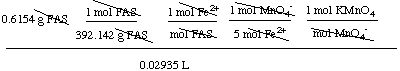Hints for Assignment 6 1998-1999

1. Hint. See examples on p. 214, Kotz and Treichel

2. Example. You have a solution of 0.2009 M chromium(III) nitrate.

(a) How many moles of solute are contained in 90.00 mL of solution?

(b) How many grams of solute are contained in 90.00 mL of solution?

(c) What volume (in milliliters) of solution is needed to obtain 0.0248 moles of solute?

Solution. Remember the definition of molarity (M): moles of solute in one liter of solution. Cr(NO₃)₃ is the solute. Thus,

moles Cr(NO₃)₃ = (molarity)(volume of solution)

(a) moles Cr(NO₃)₃ = (0.2009 mol Cr(NO₃)₃ /L)(0.09000 L)

= 0.01808 moles Cr(NO₃)₃

(b) mass Cr(NO₃)₃ = (238.01 g Cr(NO₃)₃ / mol)( 0.01808 mol)

= 4.303 g

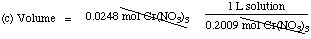
= 0.1234 L = 123 mL

3. Hint. See Example 5.10 on pp. 218-9, Kotz and Treichel. Also the Problem-Solving Tips and Ideas on p. 238.

4. Worked Example. Suppose you need 0.500 L of 1.50 M NH₃, but only the concentrated base (14.8 M) is available. What volume of the concentrated base (in mL) must you dilute to 0.500 L to obtain 1.50 M NH₃?

Solution. You know how many moles of ammonia you need in the final solution (0.500 L x 1.50 mol/L), so you have to add this many moles of ammonia as the concentrated base.

moles NH₃ needed = 0.500 L x 1.50 mol/L = 0.750 mol NH₃

You also know that one liter of the concentrated ammonia provides 14.8 mol NH₃. Thus

(0.750 mol NH₃) x (1 L concentrated base / 14.8 mol) x (1000 mL / L)

= 50.7 mL concentrated NH₃ is needed for dilution.

5. Worked Example. Suppose that 0.500 L of 3.00 M NH₃ is mixed with 0.750 L of 1.00 M NH₃. Assuming the total volume of the solution after mixing is 1.250 L, what is the concentration (molarity) of NH₃ in the resulting solution?

Solution. Find the moles of NH₃ in each of the starting solutions. Add them to get total moles, and divide by the final volume for molarity.

total moles NH₃ = (0.500 L) (3.00 mol NH₃/L) + (0.750 L) (1.00 mol NH₃/L)

= 2.25 mol NH₃

molarity of the final solution = 2.25 mol NH₃ / 1.25 L

= 1.80 M

 

6. Worked Example. What volumes of 1.50 M NH₃ and 6.00 M NH₃ must be mixed to make 0.500 L of 2.50 M NH₃?

Solution. The solution to this problem is the reverse of the one above. We have two unknowns, the volumes of the two starting solutions. However, we know that the final volume (0.500 L) is the sum of the two initial volumes:

0.500 L = volume of 1.50 M NH₃ + volume of 6.00 M NH₃ (equation 1)

We also know that the total number of moles in the final solution is equal to the sum of the moles from the two initial solutions:

(0.500 L)(2.50 mol/L) = total moles = 1.25 moles NH₃

= moles from 1.50 M NH₃ + moles from 6.00 M NH₃ (equation 2)

Let x be the volume of 1.50 M NH₃. Then from equation 1,

0.500 L = x + volume of 6.00 M NH₃, or

volume of 6.00 M NH₃ = 0.500 - x

Now use equation 2:

1.25 moles NH₃ = (x) (1.50 mol NH₃/L) + (0.500 - x)(6.00 mol NH₃/L)

Solve for x to get the answers:

x = 0.389 L of 1.50 M NH₃

0.500 - x = 0.111 L of 6.00 M NH₃

7. Hints. The following steps are necessary to solve this problem.

(a) Make sure your equation is balanced.

(b) Determine the moles of one reactant from its volume and molarity.

(c) Use the balanced equation to determine how many moles of the second reactant are needed to react with the moles of the first reactant (found in part b).

(d) Remember to convert moles of the second reactant to grams.

 

8. Hints and worked example

Hints for parts (a) and (b). Parts (a) and (b) are like parts (a) and (b) of Question 4, Assignment 4, once you determine moles of the two reactants. [To remind yourself about limiting reagent problems, click here to go to Assignment 4.]

Worked example for part (c) Suppose you mix 25.0 mL of 0.1500 M Ba(NO₃)₂ with 15.0 mL of 0.1000 M Fe₂(SO₄)₃ . What is the molarity of the excess reactant remaining in solution after the maximum mass of BaSO₄ has precipitated? The balanced equation is

3 Ba(NO₃)₂ + Fe₂(SO₄)₃ Æ 3 BaSO₄ + 2 Fe(NO₃)₃

Solution: Step 1: First determine the reactant that is in excess [you will have done this already in order to do part (a)]

moles Ba(NO₃)₂ = (0.0250 L) x (0.1500 mol / L) = 0.00375 moles

moles Fe₂(SO₄)₃ = (0.0150 L) x (0.1000 mol / L) = 0.00150 moles

moles Ba(NO₃)₂ needed to react with 0.00150 moles Fe₂(SO₄)₃:

0.00150 mol Fe₂(SO₄)₃ x (3 mol Ba(NO₃)₂/mol Fe₂(SO₄)₃)

= 0.00450 mol Ba(NO₃)₂ needed

We don't have this much Ba(NO₃)₂ so Ba(NO₃)₂ is limiting and Fe₂(SO₄)₃ is in excess

Step 2: Determine how much Fe₂(SO₄)₃ reacts with the Ba(NO₃)₂:

0.00375 mol Ba(NO₃)₂ x (1 mol Fe₂(SO₄)₃/ 3 mol Ba(NO₃)₂)

= 0.00125 mol Fe₂(SO₄)₃ reacts

Step 3: Determine the molarity of the excess Fe₂(SO₄)₃.

Amount of Fe₂(SO₄)₃ remaining = amount to start - amount reacted

= 0.00150 mol - 0.00125 mol = 0.00025 mol (2 s.f. now!)

Final volume of solution = 15.0 mL + 25.0 mL = 40.0 mL = 0.0400 L

Therefore the molarity of the Fe₂(SO₄)₃ after the reaction is:

0.00025 mol Fe₂(SO₄)₃ / 0.0400 L = 0.0063 M (2 s.f.)

9. Hints.

Step 1. Find the moles of one of the reactants fron the known volume and molarity. Remember, you can't find the moles of the other reactant directly because you only know the mass of the entire sample, not the mass of the specific compound.

Step 2. Use the equation (stoichiometric ratio) to find moles of the other reactant.

Step 3. Calculate the mass of the other reactant now that you know the moles

Step 4. Determine its percentage in the original sample.

10. Hints. Determine the moles of sodium hydroxide from the volume and molarity, and use the balanced equation to get the moles of the unknown acid. Remember that the molar mass is the mass in grams divided by the number of moles.

11. Worked Example. A sample of ferrous ammonium sulfate hexahydrate (Fe(NH₄)₂(SO₄)₂.6H₂O, FAS) weighed 0.6154 g. It required 29.35 mL of a potassium permanganate solution for titration. What is the molarity of the KMnO₄ solution? The net ionic equation for the reaction is:

5 Fe²⁺ + MnO₄^- + 8 H⁺ Æ 5 Fe³⁺ + Mn²⁺ + 4 H₂O

The molar mass of Fe(NH₄)₂(SO₄)₂.6H₂O is 392.142 g/mol.

Analysis of the problem. You can calculate the moles of ferrous ammonium sulfate hexahydrate since you know its mass. From this and the balanced equation you can determine the moles of permanganate, and from the moles and volume of the potassium permanganate you can get the molarity.

Solution.

moles FAS = (0.6154 g) x (1 mol / 392.142 g)

= 0.001569329 mol

moles Fe²⁺ = moles FAS x (1 mol Fe²⁺ / mol FAS)

= 0.001569329 mol

moles MnO₄^- = 0.001569329 mol Fe²⁺ x (1 mol MnO₄^- / 5 mol Fe²⁺ )

= 0.000313866 mol

moles KMnO₄ = 0.000313866 mol MnO₄^- x (1 mol KMnO₄ / mol MnO₄^- )

= 0.000313866 mol

molarity of KMnO₄ = moles KMnO₄ / volume of KMnO₄ (in L)

= 0.000313866 mol / 0.02935 L

= 0.010693898 M

= 0.01069 M (after rounding)

Note: for those adept at using dimensional analysis, this question can be worked in a single step:

molarity of KMnO₄ =

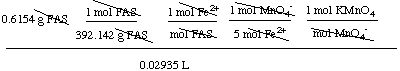
= 0.01069 M (after rounding)

12. Worked Example. A sample weighing 0.9513 g contains an unknown amount of Fe(NH₄)₂(SO₄)₂.6H₂O. The sample required 38.75 mL of 0.01069 M KMnO₄ for titration.

(a) What is the percentage of Fe(NH₄)₂(SO₄)₂.6H₂O in the sample?

(b) What is the percentage of Fe in the sample?

Analysis of the problem. Now we know the molarity and volume of potassium permanganate, but we do not know how much FAS we had to begin with. This can be calculated by a series of steps that are the inverse of Question 12.

The molar mass and balanced equation are given in Question 12.

Solution, part (a).

moles MnO₄^- = moles KMnO₄ (1 mol MnO₄^- / 1 mol KMnO₄ )

= 0.03875 L x (0.01069 mol KMnO₄ / L)

= 0.00041424 mol MnO₄^-

moles Fe²⁺ = moles MnO₄^- x (5 mol Fe²⁺ / mol MnO₄^- )

= 0.00041424 mol MnO₄^- x (5 mol Fe²⁺ / mol MnO₄^- )

= 0.0020712 mol Fe²⁺

And since each mole of Fe(NH₄)₂(SO₄)₂.6H₂O (FAS) contains one mole of Fe²⁺,

moles FAS = moles Fe²⁺

mass FAS = 0.0020712 mol FAS x 392.142 g/mol

= 0.8121996 g

% FAS = 100 * 0.8121996 g FAS / 0.9513 g sample

= 85.38 % FAS

Solution, part (b).

% Fe = 100 * mass Fe / mass sample

You know that one mole (392.142 g) of FAS contains one mole (55.847 g) of iron. Therefore,

mass Fe = mass FAS x (55.847 g Fe / 392.142 g FAS) = 0.11567 g Fe

Therefore % Fe = 100 x 0.11567 g Fe / 0.9513 g sample

= 12.16 % Fe

 

13. Worked Example. Sodium thiosulfate, Na₂S₂O₃, is an important reagent for titrations. Its solutions can be standardized by titrating the iodine released when a weighed amount of potassium hydrogen iodate, KH(IO₃)₂ (389.912 g/mol), is allowed to react with potassium iodide in acidic solutions. The net ionic equations are:

production of iodine from KH(IO₃)₂: IO₃^- + 5 I^- + 6 H⁺ Æ 3 I₂ + 6 H₂O

titration of iodine: I₂ + 2 S₂O₃^2- Æ 2 I^- + S₄O₆^2-

What is the molarity of a sodium thiosulfate solution if 27.62 mL are required to titrate the iodine released from 0.1695 g of KH(IO₃)₂?

Analysis of the Question. There are 3 important differences between this question and Question 12.

1. The reaction occurs in two different stages.

2. The product of the first reaction (I₂) is titrated in the second

3. There are TWO moles of iodate in one mole of KH(IO₃)₂

Thus, we have to connect what we begin with [KH(IO₃)₂] to the amount of iodine produced in the first step. Then we can calculate the moles of thiosulfate that reacted, and from that obtain the molarity of Na₂S₂O₃.

Solution. First find the moles of iodate:

moles IO₃^- =

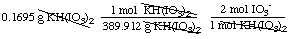
= 0.00086943 mol IO₃^-

 

Now find the moles of I₂ produced from this amount of iodate:

moles I₂ produced = 0.00086943 mol IO₃^- x (3 mol I₂ / 1 mol IO₃^- )

= 0.0026083 mol I₂

Next use the second equation to determine the amount of thiosulfate needed for titration:

moles S₂O₃^2- = 0. 0023082 mol I₂ x (2 mol S₂O₃^2- / mol I₂ )

= 0.0052166 mol S₂O₃^2-

= 0.0052166 mol Na₂S₂O₃ (1 mol S₂O₃^2- in each mol of Na₂S₂O₃ )

Molarity of Na₂S₂O₃ = moles Na₂S₂O₃ / volume used for titration

= 0.0052166 mol / 0.02762 L

= 0.1889 M Na₂S₂O₃

 

This page is http://chemiris.labs.brocku.ca/~chemweb/courses/chem180/CHEM_1P80_Assign_6.html
Last revised: October 23 2000 by M. F. Richardson
© Brock University, 1999