Lecture 11

Crystal Field Thory for Tetrahedral and Square Complexes
A. Tetrahedral Complexes

B. Square Planar Complexes

A. Tetrahedral Complexes

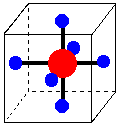
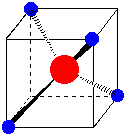
1. d-Orbital Splitting in Tetrahedral Coordination. A cube, an octahedron, and a tetrahedron are related geometrically. Octahedral coordination results when ligands are placed in the centers of cube faces. Tetrahedral coordination results when ligands are placed on alternate corners of a cube.

 
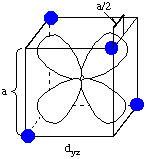
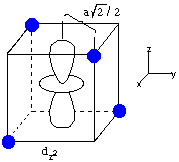
Octahedral complex in a cube. Ligands are on the centers of the cube faces.
Tetrahedral complex in a cube. Ligands are on alternate corners of the cube.
Now consider the effect of the ligands on the energies of the d-orbitals in tetrahedral coordination, with the dyz and dz2 orbitals as examples. An electron in the dyz orbital can approach the ligand to within a distance of a/2, where a is the cube edge length. However, an electron in dz2 only approaches the ligands at a distance of a/2(20.5), a distance 1.414 times as long as the distance in the dyz case. This means that the dz2 orbital is lower in energy than the dyz orbital, exactly the opposite case as in octahedral coordination.
The dyz orbital in tetrahedral coordination. Electrons in this orbital can approach within a distance of a/2 to ligand electrons.
The dz2 orbital in tetrahedral coordination: electrons in dz2 are further from the ligands than electrons in dyz.

The dxz and dxy orbitals behave the same way as dyz, and dx2-y2 behaves the same way as dz2. The resulting d-orbital splitting diagram for tetrahedral coordination is the inverse of the diagram for octahedral coordination, as shown below.

 

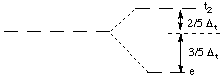
The energy difference between the t2 and the e orbitals is called the tetrahedral splitting energy.

 The dxy, dxz, and dyz orbitals are the t2 orbitals, and they are higher in energy than the e orbitals (dz2 and dx2-y2) in tetrahedral coordination. 
(Note that the orbitals are labelled t2 and e, not t2g and eg; g refers to a geometry, such as octahedral, that has a center of symmetry. The tetrahedral geometry has no center of symmetry).
 
 

2. Crystal Field Stabilization Energy in Tetrahedral Complexes. The tetrahedral crystal field stabilization energy is calculated the same way as the octahedral crystal field stabilization energy. The magnitude of the tetrahedral splitting energy is only 4/9 of the octahedral splitting energy, or

As a result of the relatively small size of the tetrahedral splitting energy, there are no low-spin tetrahedral complexes. It is always more energetically favorable to put an electron into a t2 orbital rather than pair it in an e orbital.

Let's calculate the crystal field stabilization energy for a tetrahedral cobalt(II) complex. Cobalt(II) is a d7 ion. The electronic configurations of the free ion and the tetrahedral complex are shown below.

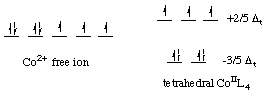
A table showing the crystal field stabilization energies for tetrahedral complexes with different numbers of d-electrons is given below.

Crystal Field Stabilization Energies for Tetrahedral Complexes of d1 - d10 Ions

# of d-electrons
Tetrahedral CFSE
# of d-electrons
Tetrahedral CFSE
1
-0.6 Deltat
6
-0.6 Deltat
2
-1.2 Deltat
7
-1.2 Deltat
3
-0.8 Deltat
8
-0.8 Deltat
4
-0.4 Deltat
9
-0.4 Deltat
5
zero
10
zero

 

B. Square Planar Complexes

1. d-Orbital Splitting in Square Planar Coordination. Square planar coordination can be imagined to result when two ligands on the z-axis of an octahedron are removed from the complex, leaving only the ligands in the x-y plane. As the z-ligands move away, the ligands in the square plane move a little closer to the metal.

The orbital splitting diagram for square planar coordination can thus be derived from the octahedral diagram. As ligands move away along the z-axis, d-orbitals with a z-component will fall in energy. The dz2 orbital falls the most, as its electrons are concentrated in lobes along the z-axis. The dxz and dyz orbitals also drop in energy, but not as much. Conversely, the dx2-y2 and the dxy orbitals increase in energy. The splitting diagram for square planar complexes is more complex than for octahedral and tetrahedral complexes, and is shown below with the relative energies of each orbital.

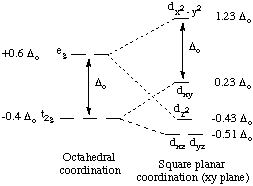
2. Crystal Field Stabilization Energy in Square Planar Complexes. Square planar coordination is rare except for d8 metal ions. Among the d8 metal ions exhibiting square planar coordination are nickel(II), palladium(II), platinum(II), rhodium(I), iridium(I), copper(III), silver(III), and gold(III). Copper(II) and silver(II), both d9 ions, are occasionally found in square planar coordination.

All known square planar complexes of d8 ions are diamagnetic, because the highest-energy orbital (dx2-y2) is greatly destabilized, and pairing in the dxy orbital is more favorable than placing an unpaired electron in the dx2-y2 orbital.

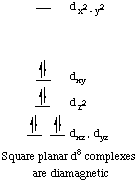
The crystal field stabilization energy for a diamagnetic square planar d8 metal complex is readily calculated by the usual method:

The pairing energy correction is included because a free d8 ion has 2 unpaired electrons, but a square planar d8 complex has no unpaired electrons.
 
 

Back to Lecture Schedule

Back to CHEM 2P32 Home Page

This page is http://chemiris.labs.brocku.ca/~chemweb/courses/chem232/CHEM2P32_Lecture_11.html
Created January 28, 2001 by M. F. Richardson
© Brock University, 2001