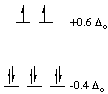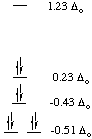B. Preferred Geometries: Octahedral Site Preference Energy (OSPE)

C. Preferred Geometries: Why Square Planar Nickel and Platinum?

D. Variations in Reactivity

1. Number of ligand atoms coordinated to the metal (the coordination number). Other things being equal, the more ligands that are coordinated, the greater the bond energy. Thus 6-coordinate complexes are inherently more stable than 4-coordinate complexes, but not by the ratio of 6:4 because of the next factor.

2. Bond energy for each M-L bond. The greater the bond energy, the more stable the complex. This factor interacts with the first. Four-coordinate complexes have shorter bonds than six-coordinate complexes, and shorter bonds are stronger bonds. For a divalent ion such as Ni(II), the estimated bond energy for each Ni-OH₂ bond in [Ni(H₂O)₆]²⁺ is about 300 kJ/mol; for the tetraaquo complex in either tetrahedral or square geometry it is about 350 kJ/mol. [Estimated from hydration energy for the Ni(II) ion.]

3. Inherent nature of the ligand. Chelating ligands are an example here; complexes of polydentate ligands are more stable than corresponding monodentate complexes (e.g. octahedral [Ni(en)₃]²⁺ is more stable than octahedral [Ni(NH₃)₆]²⁺). But there are other, more subtle examples. For example, complexes of NH₃ are more stable than complexes of N-bonded NCS^-. And certain metal ions prefer specific donor atoms over others, which we will learn more about later on in the course when we study Hard-Soft Acid-Base Theory.

4. The crystal field stabilization energy (CFSE). It is possible to calculate CFSE's in any geometry in terms of the octahedral splitting energy Delta_o; we've shown how to do it for three common geometries: octahedral, tetrahedral, and square. Clearly, the CFSE is important, and it depends on the number of d-electrons, and which orbitals they occupy.

However, it's not just the CFSE in terms of Delta_o that we need, it's the value in kJ/mol, and that depends on the actual magnitude of Delta_o for a given complex. Remember that Delta_o depends on these factors:

• The specific metal ion. Even if two metal ions have the same charge and the same ligands, and are in the same period of the periodic table, they can have different values of Delta_o. Some examples:

Metal Complex
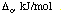
[Cr(H2O)6]2+	166
[Mn(H2O)6]2+	93
[Fe(H2O)6]2+	124
[Ni(H2O)6]2+	111

• The charge on the metal ion. We've seen in a previous lecture that the charge on the metal ion affects the value of Delta_o for a given set of ligands.

Complex
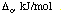
[Co(NH3)6]2+	121
[Co(NH3)6]3+	274

• The period number of the metal ion for metals in the same group. We've also seen that the octahedral splitting increases by about 50% on going from the 4th period to the 5th, and by another 25% on going from the 5th period to the 6th.

Complex
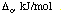
[Co(NH3)6]3+	274
[Rh(NH3)6]3+	408
[Ir(NH3)6]3+	491

• The nature of the ligand. This is just a restatement of the spectrochemical series, that ligands can be arranged in order of their ability to split the d-orbitals.

Complex
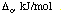
[CrCl6]3-	158
[Cr(H2O)6]3+	208
[Cr(NH3)6]3+	257
[Cr(en)6]3+	262
[Cr(CN)6]3-	318

In Lecture 8 we raised several questions that we wanted a bonding theory to explain. One of them had to do with the pronounced preference of some metal ions for a specific coordination number and geometry. For example:

• Cr³⁺, Co³⁺, and Pt⁴⁺ were cited as ions that are found almost exclusively in octahedral coordination.
• On the other hand, Pt²⁺ was stated to be an ion that occurred only in square planar coordination. Other ions that occur only in square planar coordination include Au³⁺, Rh⁺, and Ir⁺.
• A few metal ions (high-spin Fe³⁺, high-spin Mn²⁺, and Zn²⁺ among them) seem to have a fair proportion of tetrahedral complexes in addition to octahedral complexes, but no square planar complexes.

There is a correlation between electronic configuration and preferred geometries. Ions from different groups and different periods in the periodic table have similar properties based on the number of d-electrons and the crystal field stabilization energies.

1. The octahedral site preference energy (OSPE) for Co(III) and other low-spin d⁶ ions is very large. The CFSE can be calculated for octahedral and tetrahedral cobalt(III) complexes as shown in the Figure below. The octahedral complex is much more stabilized by the d-orbital splittings than the tetrahedral complex. This

The difference between the crystal field stabilization energies for an octahedral complex and a complex in another geometry (tetrahedral in this case) is called the octahedral site preference energy. The actual magnitude of the difference above, -2.13 Delta_o, is several hundred kilojoules since the octahedral splitting energy varies from about 60 kJ for the weakest ligands to more than 300 kJ for the strongest.

Thus, not only is octahedral coordination for Co(III) favored by the larger number of bonds compared to tetrahedral complexes, but also by the CFSE.
 
 

2. The octahedral site preference energy (compared to tetrahedral coordination) is also very large for Cr(III) and other d³ ions, and for low-spin complexes of d⁴, d⁵, and d⁷ ions.

The graph below gives the OSPE in terms of Delta_o for every d-electron configuration. Again, octahedral coordination is not only favored by the greater number of bonds compared to tetrahedral, but also by the greater crystal field stabilization energy for octahedral d³ and low-spin d⁴, d⁵, and d⁷ complexes. It is not surprising that there are so many octahedral complexes for these ions.

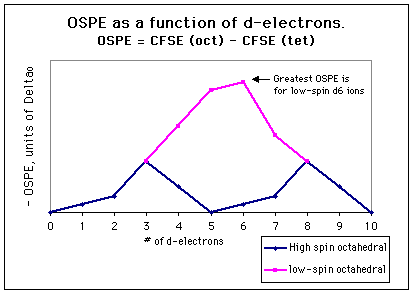
3. Some metal ions have no electronic preference for octahedral coordination over tetrahedral coordination. For high-spin d⁵ complexes, d⁰ complexes, and d¹⁰ complexes, there is no difference in the crystal field stabilization energies in octahedral and tetrahedral geometries; they are zero in both geometries. The OSPE is small even for d¹, d², and high-spin d⁶ and d⁷ ions. Ions with these d-electron configurations are the most likely to be associated with tetrahedral complexes, as factors other than electronic structure determine the preferred geometry. Among the d⁰ ions are Ti(IV), V(V), and Mo(VI); the most common d⁵ ions are Mn(II) and Fe(III); and Zn(II), Cd(II), Hg(II), Cu(I), Ag(I), and Au(I) are the most common d¹⁰ ions. Many tetrahedral complexes are known for these ions.
 
 

Let's consider a single example. Nickel forms the octahedral hexaammine complex, [Ni(NH₃)₆]²⁺, but platinum forms the square planar tetraammine complex [Pt(NH₃)₄]²⁺. Both metal ions have 8 d-electrons. We can calculate a preference energy for octahedral over square planar coordination, just as we did for octahedral over tetrahedral. We will neglect the pairing energy for this calculation.

 

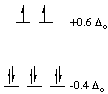
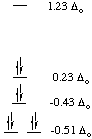
CFSEoct = -1.2 Deltao	CFSEsq.pl. = -2.44 Deltao

Notice that in this case, the crystal field stabilization (in terms of Delta_o) is much greater for square planar coordination than for octahedral coordination! In fact, the preference energy (compared to octahedral coordination) for square planar coordination of a d8 metal ion is -1.24 Delta_o. However, let's use the following values and determine the absolute values for the square planar preference in kJ/mol.

 

Complex
[Ni(NH3)x]2+	132
[Pt(NH3)x]2+	359

Preference for square planar coordination by [Ni(NH₃)_x]²⁺ = -1.24 (132 kJ/mol)

= -164 kJ/mol

Preference for square planar coordination by [Pt(NH₃)_x]²⁺ = -1.24 (359 kJ/mol)

= -445 kJ/mol

Thus square planar [Pt(NH₃)₄]²⁺ is stabilized by nearly 300 kJ/mol more than the corresponding nickel complex. This greater energy difference is enough to make up for the loss in bond energy suffered as an octahedral platinum(II) complex is transformed to a square planar complex, but is not usually enough to favor square planar complexes for nickel.

So why does nickel form square planar complexes at all? Actually, there are many fewer square planar complexes than there are octahedral ones. the ones that are square planar tend to be found with stronger-field ligands, i.e. those that are capable of giving high values for the octahedral splitting energy Delta_o.

Let's take as a single example the difference in ligand substitution rates for the complexes [Co(NH₃)₆]³⁺ and [Ni(NH₃)₆]²⁺. Each complex has a negative enthalpy for the following reaction, so both complexes are thermodynamically capable of undergoing ligand exchange with water.

[M(NH₃)₆]ⁿ⁺ + 6 H₃O⁺ ---> [M(H₂O)₆]ⁿ⁺ + 6 NH₄⁺

However, the exchange reaction for the nickel complex is very fast, while the reaction for the cobalt complex takes days or weeks to go to completion. Why is this?

The short answer is found if we consider the reaction mechanism, i.e., how the reaction must take place. There are two limiting possibilities, both of them involving a 2-step reaction as shown below.

Mechanism 1. One of the NH₃ ligands dissociates from the complex to give a 5-coordinate intermediate. This intermediate then forms a complex with a water molecule.
[M(NH₃)₆]ⁿ⁺ ---> [M(NH₃)₅]ⁿ⁺ + NH₃

Repetition of this process ultimately gives the hexaaquo ion.

Mechanism 2. A water molecule coordinates to the complex to give a 7-coordinate intermediate. This intermediate then loses an ammonia molecule.

The process repeats itself until the hexaaquo ion is formed.

Each of these mechanisms involves a reaction to give a reactive intermediate with a different coordination number (5 or 7).

When M = Co(III) (low-spin d⁶), considerable crystal field stabilization is lost because the CFSE is so much greater for octahedral coordination than the CFSE than any possible geometry in 5- or 7-coordination. The loss in CFSE on going from 6-coordination to 5- or 7-coordination increases the activation energy for the reaction, thus slowing it.

For most other ions, there is less loss (or even a gain) in CFSE on going from 6- to 5- or 7-coordinate intermediates. Thus exchange reactions for these ions are not retarded by the loss in CFSE.
 
 

This page is http://chemiris.labs.brocku.ca/~chemweb/courses/chem232/CHEM2P32_Lecture_12.html
Created February 2, 2001 by M. F. Richardson.
© Brock University, 2001